CUDA approfondi

CuBLAS est une implémentation de BLAS pour CUDA, qui s'utilise donc sur GPU. Mais qu'est-ce que BLAS ?

Il s'agit d'un ensemble de fonctions standardisées, initialement prévues pour le Fortran, qui servent au calcul algébrique linéaire basique, comme les multiplications de matrices ou de vecteurs.

BLAS n'est pas une librairie en tant que telle : il ne s'agit que d'un standard, qui doit encore être implémenté. En voici quelques-unes, parmi les principales.

• refblas, l'implémentation de référence ;
• ACML, optimisée par AMD ;
• Accelerate, optimisée par Apple ;
• MKL, optimisée par Intel ;
• CuBLAS, prévue pour CUDA, que nous allons étudier.

Cette librairie, comme les deux autres, n'est prévue que pour être utilisée conjointement à CUDA ! Elle peut être utilisée en solo, c'est pour cela qu'elle a été prévue, mais elle peut aussi très bien utiliser des emplacement de mémoire déjà alloués par CUDA !

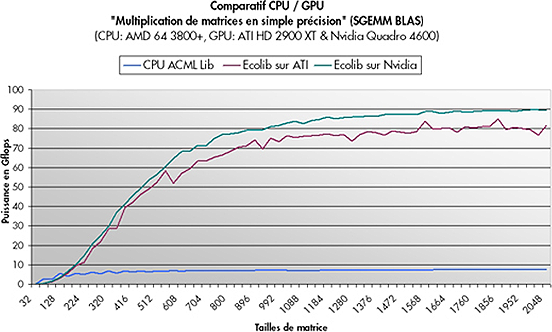
L'implémentation qui est proposée par NVIDIA est, évidemment, optimisée pour les GPU NVIDIA. Ce graphique montre les gains que l'on peut espérer en retirer, face à l'ACML, en utilisant Ecolib, une librairie de calcul spécialement prévue pour les GPU, qui utilise CuBLAS.

Comme vous pouvez voir, dans le cas de multiplications de matrices, les gains peuvent être énormes, s'il y a assez de données en entrée. En effet, pour multiplier de petites matrices, les temps d'envoi des données à la carte graphique et d'initialisation du kernel peuvent être démesurés.

Pourquoi avoir choisi cette librairie pour le comparatif ?
Ceux qui l'ont écrite sont des professionnels, qui passent leur temps à optimiser leurs algorithmes, que ce soit pour le GPU ou pour le CPU. On peut donc dire que ce test est fiable, vu que les méthodes de calcul pour CPU et GPU sont optimisées à un très haut niveau, dans les deux cas.

Cependant, lorsque vous ajoutez le fait que les résultats doivent être transportés du GPU vers le CPU, le tableau devient moins parfait.

BLAS est constitué de 3 niveaux de fonctions, chacun s'occupant de certains calculs.

Le premier niveau prend en charge les opérations entre vecteurs, comme le produit scalaire, ou la norme, de cette forme.

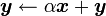
Le second niveau prend en charge les opérations entre vecteurs et matrices, de cette forme.

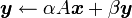
Mais aussi les opérations avec une matrice triangulaire de cette forme.

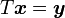
Le troisième niveau prend en charge les opérations entre matrices, de cette forme.

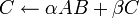
Mais aussi les opérations avec une matrice triangulaire de cette forme.

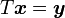
C'est ce niveau trois qui est utilisé pour la multiplication de matrices générales (alias GEMM).

Cette librairie a besoin d'une initialisation en bonne et due forme, mais celle-ci est extrêmement simple.

cublasInit();

Et c'est fait !

Cependant, il peut arriver qu'il y ait des erreurs à l'initialisation. Elles sont renvoyées directement par la fonction. Il n'y a que deux retours possibles à ce stade.

• CUBLAS_STATUS_ALLOC_FAILED : erreur à l'allocation des ressources ;
• CUBLAS_STATUS_SUCCESS : succès.

Et quand la librairie ne sera plus utilisée, il est préférable de l'éteindre.

cublasShutdown();

Ceci peut aussi amener son lot d'erreurs.

• CUBLAS_STATUS_NOT_INITIALIZED : les ressources n'ont pas encore été allouées ;
• CUBLAS_STATUS_SUCCESS : succès.

Néanmoins, la récupération des erreurs des autres fonctions de CUBLAS n'est pas aussi facile : les fonctions ne retournent rien elles-mêmes. Il faut faire appel à cublasGetError() pour récupérer l'erreur. Dès qu'une erreur est lue, l'état est remis à CUBLAS_STATUS_SUCCESS, c'est-à-dire succès.

CUBLAS peut s'interfacer avec CUDA même s'il n'est pas fait pour ça à l'origine. Des blocs mémoires alloués avec CUDA peuvent être utilisés avec CuBLAS.

BLAS fonctionne avec deux types de valeurs : des vecteurs et des matrices. CUBLAS permet donc de travailler avec ces types. Avant de leur mettre une valeur, on commence par allouer un espace en mémoire, puis on le spécialise.

Nous allons ici créer une matrice et la remplir.

// Constantes
#define    N    (2);      // Nombre de lignes et de colonnes de la matrice
#define    N2   (N * N);  // Produit du nombre de lignes et de colonnes

// Allocation de la mémoire pour la matrice sur l'hôte
float *      hote;
hote    = (float *) malloc ( N2 * hote[0] );

// Remplissage de la matrice
hote[0] = 14 ;        // 1 1
hote[1] = 54 ;        // 1 2
hote[2] = 29 ;        // 2 1
hote[3] = 36 ;        // 2 2

// Allocation de la mémoire pour la matrice sur le périphérique
float *    periph = 0;
cublasAlloc(N2, sizeof(periph[0]), (void * *) & periph);

// Copie de la matrice de l'hôte vers le périphérique
cublasSetVector(N2, sizeof(hote[0]), hote[0], 1, periph[0], 1);

// Destruction de la matrice sur l'hôte
free(hote);

// Destruction de la matrice sur le périphérique
cublasFree(periph);

CUBLAS ne s'occupe que de matrices dites "colonnes majeures". C'est pourquoi il faut préciser le nombre de lignes. En connaissant le nombre de lignes, on connaît le nombre de colonnes, vu que l'on a l'ensemble des valeurs de la matrice. Ceci nous permet d'utiliser un simple tableau de flottants : chaque valeur du tableau correspond à une valeur de la matrice.

cublasAlloc() crée donc un tableau en mémoire. Les propriétés de ce tableau sont dictées par les paramètres de la fonction.

1. int : nombre de cases du tableau ;
2. int : taille d'un élément du tableau ;
3. void * * : pointeur vers la mémoire à allouer.

cublasSetVector() spécialise ce tableau en vecteur (qui n'est qu'une forme simplifiée de matrice). Voici ses quelques paramètres.

1. int : nombre d'éléments à copier du vecteur hôte ;
2. int : taille d'un élément de chaque côté ;
3. const void * : vecteur hôte ;
4. int : nombre d'espaces entre les valeurs du vecteur hôte ;
5. void * : vecteur périphérique ;
6. int : nombre d'espaces entre les valeurs du vecteur péripérique.

Quand le vecteur est une matrice, ou une partie d'une matrice, l'incrément du vecteur de 1 permet d'accéder à une colonne, de la dimension majeure de la matrice (son nombre de colonnes ou de lignes), à une ligne.

cublasGetVector() fonctionne de manière analogue : le premier vecteur est celui qui va être copié, le second, l'emplacement où le premier va être stocké.

Pour initialiser une vraie matrice, nous pouvons utiliser la fonction cublasSetMatrix(). Voici son prototype.

cublasSetMatrix
(
    int rows,
    int cols,
    int elemSize,
    const void *A,
    int lda,
    void *B,
    int ldb
)

• rows : nombre de colonnes ;
• cols : nombre de lignes ;
• elemSize : taille d'un élément de la matrice ;
• A : la matrice source ;
• lda : dimension de direction de A ;
• B : matrice destination ;
• ldb : dimension de direction de B.

Un petit exemple.

// Allocation de la matrice source
   float * a;
   int rows;
   int cols;
   int lda;

   rows = 4;
   cols = 4;
   lda  = cols;

   a = (float *) malloc( sizeof(float) * rows * cols);
   
// Remplissage de la matrice source
   // Première colonne
   a[0] = 1;
   a[1] = 2;
   a[2] = 3;
   a[3] = 4;
   // Deuxième colonne
   a[rows    ] = 1;
   a[rows + 1] = 1;
   a[rows + 2] = 1;
   a[rows + 3] = 1;
   // Troisième colonne
   a[rows * 2    ] = 3;
   a[rows * 2 + 1] = 4;  
   a[rows * 2 + 2] = 5;
   a[rows * 2 + 3] = 6;
   // Quatrième colonne
   a[rows * 3    ] = 5;
   a[rows * 3 + 1] = 6;
   a[rows * 3 + 2] = 7;
   a[rows * 3 + 3] = 8;

// Allocation de la matrice destination
   float *    b = 0;
   cublasAlloc(rows * cols, sizeof(b[0]), (void * *) & b);

// Copie de la matrice
   cublasSetMatrix (rows, cols, sizeof(float), (const void *) a, lda, (void *) b, lda) ;
    
// Suppression des matrices
   cublasFree(b);
   free(a);

L'implémentation de BLAS a été effectuée à deux niveaux de précision : la précision simple (FP32) et la double précision (FP64).

Il existe aussi des séries de fonctions pour les nombres complexes.

Toutes les combinaisons n'ont pas été implémentées complètement : les fonctions complexes de BLAS1 à double précision et les fonctions complexes de BLAS2 ne le sont pas encore tout à fait. Toutes les autres le sont. Pour plus de précision, cet article précise toutes les combinaisons existantes sous CUDA 2.2.

Ceci a pour conséquence que toutes les fonctions de chaque niveau existent en 4 versions. Voici les préfixes utilisés.

• S : réel, simple précision ;
• C : complexe, simple précision ;
• D : réel, double précision ;
• Z : complexe, double précision.

Ensuite, une série de suffixes, propres à chaque niveau, complètent le nom.

Une fonction de CuBLAS aura donc cet aspect :
cublas + [SDCZ] + suffixe

Par exemple, la fonction du premier niveau qui s'occupe de réels en simple précision et qui effectue un produit scalaire est celle-ci : cublasSdot(). S spécifie le type des vecteurs, dot, l'opération à effectuer.

Il est à noter deux exceptions : les suffixes Ixamax et Ixamin, où le préfixe se met à la place du x.

CuBLAS utilise plusieurs types, deux ne sont pas issus du standard du C : cuComplex et cuDoubleComplex. Vous pouvez les créer grâce à deux fonctions.

cuFloatComplex  make_cuFloatComplex  ( float  x, float  y ) ;
cuDoubleComplex make_cuDoubleComplex ( double x, double y ) ;

Le premier nombre, x, est la partie réelle du complexe ; y, sa partie imaginaire.

Les autres types utilisés sont hérités du standard.

VII-G-1. Ixamax▲

int cublasIsamax ( int n, const float     * x, int incx ) ;
int cublasIdamax ( int n, const double    * x, int incx ) ;
int cublasIcamax ( int n, const cuComplex * x, int incx ) ;

VII-G-2. Ixamin▲

int cublasIsamin ( int n, const float     * x, int incx ) ;
int cublasIdamin ( int n, const double    * x, int incx ) ;
int cublasIcamin ( int n, const cuComplex * x, int incx ) ;

VII-G-3. asum▲

float cublasSasum  ( int n, const float    * x, int incx ) ;
float cublasDasum  ( int n, const double   * x, int incx ) ;
float cublasScasum ( int n, const cuDouble * x, int incx ) ;

VII-G-4. axpy▲

void cublasSaxpy ( int n, float     alpha, const float     * x, int incx, float     * y, int incy ) ;
void cublasDaxpy ( int n, double    alpha, const double    * x, int incx, double    * y, int incy ) ;
void cublasCaxpy ( int n, cuComplex alpha, const cuComplex * x, int incx, cuComplex * y, int incy ) ;

VII-G-5. copy▲

void cublasScopy ( int n, const float     * x, int incx, const float    * y, int incy ) ; 
void cublasDcopy ( int n, const double    * x, int incx, const double   * y, int incy ) ; 
void cublasCcopy ( int n, const cuComplex * x, int incx, const cuDouble * y, int incy ) ;

VII-G-6. dot▲

float cublasSdot ( int n, const float  * x, int incx, const float    * y, int incy ) ;
float cublasDdot ( int n, const double * x, int incx, const double   * y, int incy ) ;

VII-G-7. dotc▲

cuComplex cublasCdotc ( int n, cuComplex float * x, int incx, const float * y, int incy ) ;

VII-G-8. dotu▲

cuComplex cublasCdotu ( int n, cuComplex float * x, int incx, const float * y, int incy ) ;
cuComplex cublasZdotu ( int n, cuComplex float * x, int incx, const float * y, int incy ) ;

VII-G-9. nrm2▲

float cublasSnrm2  ( int n, const float     * x, int incx ) ;
float cublasDnrm2  ( int n, const double    * x, int incx ) ;
float cublasScnrm2 ( int n, const cuComplex * x, int incx ) ;

VII-G-10. rot▲

void cublasSrot ( int n, float     * x, int incx, float     * y, int incy, float sc, float ss ) ; 
void cublasDrot ( int n, double    * x, int incx, double    * y, int incy, float sc, float ss ) ; 
void cublasCrot ( int n, cuComplex * x, int incx, cuComplex * y, int incy, float sc, float ss ) ;

VII-G-11. rotg▲

void cublasSrotg ( float     * sa, float     * sb, float * sc, float * ss ) ; 
void cublasDrotg ( double    * sa, double    * sb, float * sc, float * ss ) ; 
void cublasCrotg ( cuComplex * sa, cuComplex * sb, float * sc, float * ss ) ;

VII-G-12. scal▲

void cublasSscal  ( int n, float           alpha, float           * x, int incx ) ;
void cublasDscal  ( int n, double          alpha, double          * x, int incx ) ;
void cublasCsscal ( int n, cuComplex       alpha, cuComplex       * x, int incx ) ;
void cublasZscal  ( int n, cuDoubleComplex alpha, cuDoubleComplex * x, int incx ) ;

VII-G-13. swap▲

void cublasSrotg ( int n, float     * x, int incx, float * y, int incy ) ; 
void cublasDrotg ( int n, double    * x, int incx, float * y, int incy ) ; 
void cublasCrotg ( int n, cuComplex * x, int incx, float * y, int incy ) ;

VII-H-1. gbmv▲

 

Sélectionnez

void cublasSgbmv ( char trans, int m, int n, int kl, int ku, float alpha, const float * A, int lda, 
    const float * x, int incx, float beta, float * y, int incy ) ;

Effectue une opération de la forme .

trans doit être une de ces valeurs.

• N ou n : la matrice 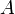ne sera pas modifiée avant calcul ;
• T ou t : la transposée de la matrice 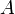sera utilisée pour les calculs ;
• C ou c : la transposée de la matrice 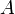sera utilisée pour les calculs.

m correspond au nombre de lignes de , n, au nombre de colonnes. Ils doivent être au minimum nuls.

kl correspond au nombre de subdiagonales de la matrice , ku, au nombre de superdiagonales de la matrice .

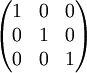
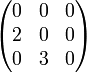
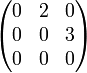
La matrice a une dimension directrice lda, qui est son nombre de lignes. lda doit au moins être égal à .

est le vecteur qui servira à la multiplication, qui doit avoir au moins dimensions si la matrice n'est pas modifée, ou si sa transposée est utilisée.

est le vecteur qui servira à la multiplication, qui doit avoir au moins dimensions si la matrice n'est pas modifée, ou si sa transposée est utilisée. C'est dans cette variable que sera stocké le résultat de l'opération.

VII-H-2. gemv▲

void cublasSgemv ( char trans, int m, int n, float alpha, const float * A, int lda,
    const float * x, int incx, float beta, float * y, int incy ) ;
void cublasDgemv ( char trans, int m, int n, float alpha, const float * A, int lda,
    const float * x, int incx, float beta, float * y, int incy ) ;
void cublasZgemv ( char trans, int m, int n, float alpha, const float * A, int lda,
    const float * x, int incx, float beta, float * y, int incy ) ;

VII-H-3. sger▲

void cublasSger ( int m, int n, float  alpha, const float  * x, int incx, const float  * y,
    int incy, float  * A, int lda ) ; 
void cublasDger ( int m, int n, double alpha, const double * x, int incx, const double * y,
    int incy, double * A, int lda ) ;

VII-H-4. sbmv▲

 

Sélectionnez

void cublasSsbmv ( char uplo, int n, int k, float alpha, const float * A, int lda,
    const float * x, int incx, float beta, float * y, int incy ) ;

Effectue les opérations de la forme , où est une matrice de de côté et symmétrique, possédant superdiagonales et subdiagonales. Par exemple, cette matrice peut servir de paramètre, à condition de donner des valeurs à , , et .

uplo doit être une de ces valeurs.

• U ou u : utiliser le triangle supérieur de la matrice (rouge) ;
• L ou l : utiliser le triangle inférieur de la matrice (vert).

VII-H-5. spmv▲

void cublasSsbmv ( char uplo, int n, float alpha, const float * AP, const float * x, int incx,
    float beta, float * y, int incy ) ;

VII-H-6. spr▲

void cublasSspr ( char uplo, int n, float alpha, const float * x, int incx, float * AP ) ;

VII-H-7. spr2▲

void cublasSspr2 ( char uplo, int n, float alpha, const float * x, int incx,
    const float * y, int incy, float * AP ) ;

VII-H-8. symv▲

void cublasSsymv ( char uplo, int n, float alpha, const float * A, int lda,
    const float * x, int incx, float beta, float * y, int incy ) ;

VII-H-9. syr▲

void cublasSsyr ( char uplo, int n, float alpha, const float * x, int incx,
    float * A, int lda ) ;

VII-H-10. syr2▲

void cublasSsyr2 ( char uplo, int n, float alpha, const float * x, int incx,
    const float * x, int incx,  float * A, int lda ) ;

VII-H-11. tbmv▲

 

Sélectionnez

void cublasStbmv ( char uplo, char trans, char diag, int n, const float * A,
    int lda, float * x, int incx ) ;

Effectue les opérations de la forme ou bien .

La matrice doit être triangulaire, c'est-à-dire semblable à celle ci-dessous.

Une matrice est dite unitriangulaire si elle est triangulaire et que toutes les valeurs de sa diagonale principale sont 1.

diag permet de spécifier si la matrice est unitriangulaire (U ou u) ou non (N ou n).

VII-H-12. tbsv▲

void cublasStbsv ( char uplo, char trans, char diag, int n, int k,
    const float * A, int lda, float * x, int incx ) ;

VII-H-13. tpmv▲

void cublasStpmv ( char uplo, char trans, char diag, int n,
    const float * AP, float * x, int incx ) ;

VII-H-14. tpsv▲

void cublasStpsv ( char uplo, char trans, char diag, int n,
    const float * AP, float * x, int incx ) ;

VII-H-15. trmv▲

void cublasStrmv ( char uplo, char trans, char diag, int n,
    const float * A, int lda, float * x, int incx ) ;

VII-H-16. trsv▲

void cublasStrsv ( char uplo, char trans, char diag, int n,
    const float * A, int lda, float * x, int incx ) ;

VII-I-1. gemm▲

void cublasSgemm ( char transa, char transb, int m, int n, int k, float alpha,
    const float * A, int lda, const float * B, int ldb,
    float beta, float * C, int ldc ) ;
void cublasDgemm ( char transa, char transb, int m, int n, int k, double alpha,
    const double * A, int lda, const double * B, int ldb,
    double beta, double * C, int ldc ) ;
void cublasCgemm ( char transa, char transb, int m, int n, int k, cuComplex alpha,
    const cuComplex * A, int lda, const cuComplex * B, int ldb,
    cuComplex beta, cuComplex * C, int ldc ) ;
void cublasZgemm ( char transa, char transb, int m, int n, int k, cuDoubleComplex alpha,
    const cuDoubleComplex * A, int lda, const cuDoubleComplex * B, int ldb,
    cuDoubleComplex beta, cuDoubleComplex * C, int ldc ) ;

VII-I-2. symm▲

void cublasSsymm ( char side, char uplo, int m, int n, float  alpha, const float  * A, int lda,
    const float  * B, int ldb, float  beta, float  * C, int ldc ) ;
void cublasDsymm ( char side, char uplo, int m, int n, double alpha, const double * A, int lda,
    const double * B, int ldb, double beta, double * C, int ldc ) ;

VII-I-3. syrk▲

void cublasSsyrk ( char uplo, char trans, int n, int k, float alpha,
    const float * A, int lda, float beta, float * C, int ldc ) ;
void cublasDsyrk ( char uplo, char trans, int n, int k, double alpha,
    const double * A, int lda, double beta, double * C, int ldc ) ;
void cublasZsyrk ( char uplo, char trans, int n, int k, cuDoubleComplex alpha,
    const cuDoubleComplex * A, int lda, cuDoubleComplex beta, cuDoubleComplex * C, int ldc ) ;

VII-I-4. syr2k▲

void cublasSsyr2k ( char uplo, char trans, int n, int k, float  alpha,
    const float  * A, int lda, const float  * B, int ldb, float  beta, float  * C, int ldc ) ;
void cublasDsyr2k ( char uplo, char trans, int n, int k, double alpha,
    const double * A, int lda, const double * B, int ldb, double beta, double * C, int ldc ) ;

VII-I-5. trmm▲

void cublasStrmm ( char side, char uplo, char transa, char diag, int m, int n, float  alpha,
    const float  * A, int lda, const float  * B, int ldb ) ;
void cublasDtrmm ( char side, char uplo, char transa, char diag, int m, int n, double alpha,
    const double * A, int lda, const double * B, int ldb ) ;

VII-I-6. trsm▲

void cublasStrsm ( char side, char uplo, char transa, char diag, int m, int n,
    float  alpha, const float  * A, int lda, float  * B, int ldb ) ;
void cublasDtrsm ( char side, char uplo, char transa, char diag, int m, int n,
    double alpha, const double * A, int lda, double * B, int ldb ) ;

Vous pouvez récupérer la dernière erreur apparue avec la fonction cublasGetError(). Celle-ci va vous renvoyer un des codes suivants (chacun accompagné de sa signification).

De l'utilisation de CuBLAS pour la multiplication de deux matrices aléatoires.

 

Cacher/Afficher le codeSélectionnez

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "cublas.h"

// Taille des matrices
#define N (275)
#define N2 (N * N);

int main(int argc, char** argv)
{
    // Déclaration des variables
    cublasStatus status;
    float *    h_A;
    float *    h_B;
    float *    h_C;
    float *    d_A        = 0;
    float *    d_B        = 0;
    float *    d_C        = 0;
    float    alpha    = 1.0f;
    float    beta    = 0.0f;
    int        i;
    
    // Initialisation de CuBLAS
    // avec gestion des erreurs
    status = cublasInit();
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'initialisation de CuBLAS !!!!!\n");
        return EXIT_FAILURE;
    }

    // Allocation de la mémoire pour les matrices sur l'hôte
    // avec gestion des erreurs
    //h_A
    h_A = (float *) malloc ( N2 * sizeof(h_A[0]) );
    if (h_A == 0)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice A sur l'hôte !!!!!\n");
        return EXIT_FAILURE;
    }
    //h_B
    h_B = (float * ) malloc ( N2 * sizeof(h_B[0]) );
    if (h_B == 0)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice B sur l'hôte !!!!!\n");
        return EXIT_FAILURE;
    }
    //h_C
    h_C = (float * ) malloc ( N2 * sizeof(h_C[0]) );
    if (h_C == 0)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice C sur l'hôte !!!!!\n");
        return EXIT_FAILURE;
    }
    
    //Remplissage des matrices avec des données aléatoires
    for (i = 0 ; i < N2 ; i++)
    {
        h_A[i] = rand() / (float) RAND_MAX;
        h_B[i] = rand() / (float) RAND_MAX;
        h_C[i] = rand() / (float) RAND_MAX;
    }
    
    // Allocation de la mémoire pour les matrices sur le périphérique
    // avec gestion des erreurs
    //d_A
    status = cublasAlloc (N2, sizeof (d_A[0]), (void **) & d_A);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice A sur le périphérique !!!!!\n");
        return EXIT_FAILURE;
    }
    //d_B
    status = cublasAlloc (N2, sizeof (d_B[0]), (void **) & d_B);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice B sur le périphérique !!!!!\n");
        return EXIT_FAILURE;
    }
    //d_C
    status = cublasAlloc (N2, sizeof (d_C[0]), (void **) & d_C);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation mémoire de la matrice C sur le périphérique !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Remplissage des matrices du périphérique avec les données des matrices de l'hôte
    // avec gestion des erreurs
    status = cublasSetVector(N2, sizeof(h_A[0]), h_A, 1, d_A, 1);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur à l'accès du périphérique lors de l'écriture de la matrice A !!!!!\n");
        return EXIT_FAILURE;
    }
    
    status = cublasSetVector(N2, sizeof(h_B[0]), h_B, 1, d_B, 1);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur à l'accès du périphérique lors de l'écriture de la matrice A !!!!!\n");
        return EXIT_FAILURE;
    }
    
    status = cublasSetVector(N2, sizeof(h_C[0]), h_C, 1, d_C, 1);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!!! Erreur à l'accès du périphérique lors de l'écriture de la matrice A !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Nettoyage de la mémoire des erreurs
    cublasGetError();
    
    // Multiplication des matrices avec CuBLAS
    cublasSgemm('n', 'n', N, N, N, alpha, d_A, N, d_B, N, beta, d_C, N);
    
    // Gestion des erreurs
    status = cublasGetError();
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!! Erreur lors de l'exécution du kernel CuBLAS !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Allocation de la mémoire sur l'hôte pour la récupération du résultat depuis le périphérique
    // avec gestion des erreurs
    h_C = (float*)malloc(N2 * sizeof(h_C[0]));
    if (h_C == 0) {
        fprintf (stderr, "!!!!! Erreur lors de l'allocation de la mémoire sur l'hôte pour la matrice C !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Lecture du résultat
    // avec gestion des erreurs
    status = cublasGetVector(N2, sizeof(h_C[0]), d_C, 1, h_C, 1);
    if (status != CUBLAS_STATUS_SUCCESS) {
        fprintf (stderr, "!!!!! Erreur d'accès au périphérique (lecture de la matrice C) !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Libération de la mémoire sur l'hôte
    free(h_A);
    free(h_B);
    free(h_C);
    
    // Libération de la mémoire sur le périphérique
    // avec gestion des erreurs
    status = cublasFree(d_A);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!! Erreur lors de la libération de l'espace périphérique pour la matrice A !!!!!\n");
        return EXIT_FAILURE;
    }
    status = cublasFree(d_B);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!! Erreur lors de la libération de l'espace périphérique pour la matrice B !!!!!\n");
        return EXIT_FAILURE;
    }
    status = cublasFree(d_C);
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!! Erreur lors de la libération de l'espace périphérique pour la matrice C !!!!!\n");
        return EXIT_FAILURE;
    }
    
    // Fermeture propre de CuBLAS
    status = cublasShutdown();
    if (status != CUBLAS_STATUS_SUCCESS)
    {
        fprintf (stderr, "!!!! Erreur à la fermeture de CuBLAS !!!!!\n");
        return EXIT_FAILURE;
    }
    
    printf("\n Appuyez sur ENTER pour quitter.\n");
    getchar();
    
    return EXIT_SUCCESS;
}

Vous avez pu remarquer que l'entièreté de CuBLAS est contenue dans le fichier cublas.h.

• refblas
• AMD ACML
• Apple Accelerate
• Intel MKL
• Ecolib

• Algèbre linéaire
• BLAS
• Produit scalaire
• Norme
• Norme euclidienne
• Nombre complexe
• Rotation plane
• Rotation de Givens
• Matrices et quaternions
• Matrice
• Ordre d'une matrice
• Matrice identité
• Diagonale d'une matrice
• Multiplication de matrices générales (GEMM)
• Transposée
• Matrice de rotation
• Conjugué

Il s'agit d'un algorithme de décomposition d'une séquence de valeurs en composants de différentes fréquences.

En pratique, cela peut servir à décomposer un signal audio pour obtenir la répartition des fréquences en fonction du temps, comme sur votre chaîne Hi-Fi, qui peut décomposer le signal transmis par les baffles en plages de fréquences : 40 Hz, 200 Hz, 1 kHz, 5kHz et 12 kHz, en général. Mais aussi pour votre électrocardiogramme !

La transformée permet d'obtenir la répartition des fréquences qui caractérisent toutes les ondes qui composent l'onde totale. Le résultat s'appelle un diffractogramme.

Cet exemple se limite aux éléments à une seule dimension. Or, notre univers est constitué de trois dimensions visibles. Cette transformée peut aussi s'appliquer à des éléments à deux ou trois dimensions.

Un exemple d'élément à deux dimensions ? Une image, tout simplement. La transformée permet de passer de l'espace réel (décrit avec des distances) à l'espace réciproque (décrit avec des fréquences). Les plus fins détails de l'image seront transcrits par les plus hautes fréquences de la réciproque.

Concernant la troisième dimension, cette transformée peut servir à la résolution d'équations différentielles partielles en trois dimensions.

Il s'agit d'un algorithme de calcul de la transformée discrète de Fourier, nettement plus rapide. Cet algorithme est le plus utilisé en traitement numérique de signal.

Cette transformée est un cas particulier des transformées de Fourier, qui translatent une fonction complexe d'une variable réelle en une autre fonction, la représentation du domaine fréquentiel (ou de fréquence), qui décrit quelles sont les fréquences dans la fonction d'origine.

Ces algorithmes (car il y en a plusieurs) sont plus rapides, mais aussi parfois plus précis dans certains cas, d'autres algorithmes permettent une approximation très approchée des valeurs réelles.

CuFFT permet, à l'heure actuelle, des transformations en une, deux ou trois dimensions, de valeurs réelles (flottantes) ou bien complexes. Des transformations à une dimension peuvent être effectuées en parallèle.

Les données à traiter sont limitées quant à leur taille : pour une seule dimension, seuls huit millions d'éléments sont supportés. Pour deux et trois dimensions, les tailles sont limitées à l'intervalle [ 2 ; 16384 ].

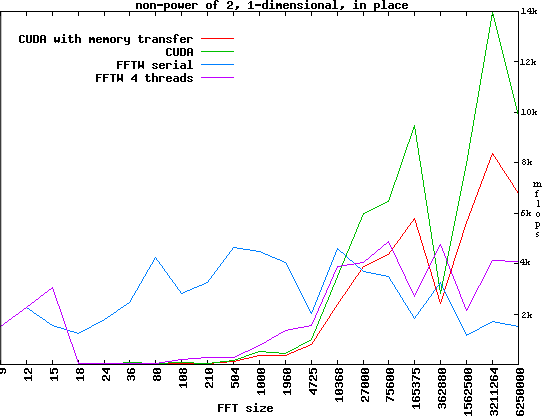
Ici, CuFFT sera comparé à FFTW, une des librairies les plus rapides pour CPU, selon les quelques comparatifs produits avec BenchFFT.

Nous pouvons voir très aisément que le CPU reste en très bonne place, pour de petites quantités de données. Cependant, lorsque l'on commence à avoir des paquets plus importants, le GPU s'impose très vite.

À propos de ce GPU, le graphique montre aussi à quel point les transferts entre CPU et GPU peuvent être lents : avec ces transferts, beaucoup moins de données sont traitées, mais toujours plus qu'un CPU, à partir d'un certain point.

Ici, CuFFT est comparé à Intel MKL, une librairie prévue pour les mathématiques (sur processeurs Intel, pour de meilleurs résultats). Ici, côté CPU, on pourrait dire que l'algorithme est très fort optimisé, mais ce n'est pas suffisant pour détrôner le GPU, qui reste le plus rapide.

CuFFT est basé sur FFTW. Ainsi, les fonctions ne traitent que des pointeurs sur des plans (* cufftHandle).

Mais qu'est-ce qu'un plan ? Un plan est une configuration pour effectuer un calcul, connue à l'avance, ce qui permet d'optimiser un maximum les calculs.

Il existe trois fonctions pour créer des plans : cufftPlan1d(), cufftPlan2d() et cufftPlan3d(), dont voici les prototypes.

cufftResult cufftPlan1d ( cufftHandle * plan, int nx,                 cufftType type, int batch ) ;
cufftResult cufftPlan3d ( cufftHandle * plan, int nx, int ny,         cufftType type            ) ;
cufftResult cufftPlan2d ( cufftHandle * plan, int nx, int ny, int nz, cufftType type            ) ;

Le plan qui sera créé aura un pointeur plan. Il contiendra nx éléments sur l'axe des abscisses, ny sur l'axe des ordonnées et nz sur l'axe des cotes (suivant le nombre de dimensions du plan). Le plan sera transformé batch fois (seulement dans le cas de plans à une dimension). Le type de transformation sera type, qui peut avoir ces quelques valeurs.

• CUFFT_C2C : complexe vers complexe ;
• CUFFT_C2R : complexe vers réel ;
• CUFFT_R2C : réel vers complexe.

Un plan peut être détruit grâce à cufftResult cufftDestroy ( cufftHandle plan ) ;.

Les valeurs des plans peuvent être, soit réelles, soit complexes. Les types associés sont cufftReal et cufftComplex.

Il existe trois fonctions permettant d'effectuer la transformation, correspondant aux trois valeurs possibles de type pour les fonctions de création de plan.

cufftResult cufftExecC2C ( cufftHandle plan, cufftComplex * idata, cufftComplex * odata, int direction ) ;
cufftResult cufftExecR2C ( cufftHandle plan, cufftReal    * idata, cufftComplex * odata                ) ;
cufftResult cufftExecC2R ( cufftHandle plan, cufftComplex * idata, cufftReal    * odata                ) ;

idata est un pointeur vers les données à traiter, odata est un pointeur vers l'emplacement où les valeurs traitées seront stockées.

direction spécifie la direction de l'algorithme : soit vers l'avant (CUFFT_FORWARD), soit vers l'arrière (CUFFT_BACKWARD).

Contrairement à CUDA et à CuBLAS, CuFFT n'utilise pas une fonction spécifique pour récupérer les erreurs. Chaque fonction renvoie un cufftResult, qui peut avoir une de ces valeurs.

• CUFFT_SUCCESS : opération effectuée correctement ;
• CUFFT_INVALID_PLAN : plan passé en argument invalide ;
• CUFFT_ALLOC_FAILED : erreur lors de l'allocation de la mémoire ;
• CUFFT_INVALID_TYPE : type demandé non supporté ;
• CUFFT_INVALID_VALUE : mauvais pointeur mémoire ;
• CUFFT_INTERNAL_ERROR : erreur interne ;
• CUFFT_EXEC_FAILED : erreur d'exécution de la transformée sur le GPU ;
• CUFFT_SETUP_FAILED : erreur d'initialisation de la librairie ;
• CUFFT_SHUTDOWN_FAILED : erreur de fermeture de la librairie ;
• CUFFT_INVALID_SIZE : taille de plan non supportée.

Pour une transformation de complexe vers complexe à une dimension, sans gestion des erreurs.

 

Cacher/Afficher le codeSélectionnez

#define NX (256)
#define BATCH (10)
#define NB (NX * BATCH)

int main()
{
    cufftHandle plan;
    cufftComplex *data;
    cudaMalloc( (void **) & data, sizeof (cufftComplex) * NB);

    cufftPlan1d(&plan, NX, CUFFT_C2C, BATCH);

    cufftExecC2C(plan, data, data, CUFFT_FORWARD);

    cufftDestroy(plan);
    cudaFree(data);
    
    return EXIT_SUCCESS;
}

Pour une transformation de complexe vers complexe à deux dimensions.

 

Cacher/Afficher le codeSélectionnez

#define NX  (256)
#define NY  (128)
#define NXY (NX * NY)

int main()
{
    cufftHandle    plan;
    cufftComplex * idata;
    cufftComplex * odata;
    
    cudaMalloc( (void **) & idata, sizeof (cufftComplex) * NXY);
    cudaMalloc( (void **) & odata, sizeof (cufftComplex) * NXY);
    
    status = cufftPlan2d(& plan, NX,NY, CUFFT_C2C);
    if (status != CUFFT_SUCCESS)
        return EXIT_FAILURE;
    
    status = cufftExecC2C(plan, idata, odata, CUFFT_FORWARD);
    if (status != CUFFT_SUCCESS)
        return EXIT_FAILURE;
    
    status cufftDestroy(plan);
    if (status != CUFFT_SUCCESS)
        return EXIT_FAILURE;
    
    cudaFree(idata);
    cudaFree(odata);
    
    return EXIT_SUCCESS;
}

Ces exemples ne disent pas une chose : pour pouvoir utiliser CuFFT, il faut inclure le fichier cufft.h.

• La transformée de Fourier en traitement d'images
• La transformée de Fourier et la transformée rapide de Fourier

• FFTW
• Utilisation de FFTW
• BenchFFT

Ces macros ne remplissent leur office que lorsque l'application est compilée en mode de débogage ! Si elle est compilée en Release, la macro n'aura aucun impact sur les performances.
En cas d'erreur, elles ferment automatiquement l'application, en même temps qu'elles écrivent dans le flux stderr.

IX-A-1. CUT_DEVICE_INIT▲

CUT_DEVICE_INIT();

There is no device.

There is no device supporting CUDA.

IX-A-2. CUDA_SAFE_CALL et CUDA_SAFE_CALL_NO_SYNC▲

CU_SAFE_CALL( cuFree );
CU_SAFE_CALL_NO_SYNC( cuFree );

Cuda runtime error %x in file __FILE__ in line __LINE__.
Cuda runtime error %x in file __FILE__ in line __LINE__.

IX-A-3. CU_SAFE_CALL et CU_SAFE_CALL_NO_SYNC▲

CU_SAFE_CALL( cuFree );
CU_SAFE_CALL_NO_SYNC( cuFree );

Cuda driver error %x in file __FILE__ in line __LINE__.
Cuda driver error %x in file __FILE__ in line __LINE__.

IX-A-4. CUT_SAFE_CALL▲

CUT_SAFE_CALL( cutFree );

Cut error in file __FILE_ in line __LINE__.

IX-A-5. CUT_CHECK_ERROR▲

CUT_CHECK_ERROR("'not enough memory'");

Cuda error: 'not enough memory' in file __FILE__ in line __LINE__ : %x.

IX-A-6. CUT_CHECK_ERROR_GL▲

CUT_CHECK_ERROR_GL();

GL Error in file __FILE__ in line __LINE__ :
%s

IX-A-7. CUFFT_SAFE_CALL▲

CUFFT_SAFE_CALL( cufftPlan1d(&plan, NX, CUFFT_C2C, BATCH) );

CUFFT error in file __FILE__ in line __LINE__.

IX-A-8. CUT_SAFE_MALLOC▲

CUT_SAFE_MALLOC( cudaMalloc( (void **) & buffer, size)) ;

Host malloc failure in file __FILE__ in line __LINE__.

IX-A-9. CUT_CONDITION▲

CUT_CONDITION(0 == 0);

IX-A-10. CUT_BANK_CHECKER▲

IX-B-1. Gestion de la mémoire▲

void cutFree ( void * ptr ) ;

IX-B-2. Gestion des fichiers▲

char * cutFindFilePath ( const char * filename, const char * executablePath ) ;

CUTBoolean cutReadFilef  ( const char * filename, float         ** data, unsigned int * len,
 bool verbose = false ) ;
CUTBoolean cutReadFiled  ( const char * filename, double        ** data, unsigned int * len,
 bool verbose = false ) ;
CUTBoolean cutReadFilei  ( const char * filename, int           ** data, unsigned int * len,
 bool verbose = false ) ;
CUTBoolean cutReadFileui ( const char * filename, unsigned int  ** data, unsigned int * len,
 bool verbose = false ) ;
CUTBoolean cutReadFileb  ( const char * filename, char          ** data, unsigned int * len,
 bool verbose = false ) ;
CUTBoolean cutReadFileub ( const char * filename, unsigned char ** data, unsigned int * len,
 bool verbose = false ) ;

CUTBoolean cutWriteFilef  ( const char * filename, const float         * data,
 unsigned int len, float         epsilon, bool verbose = false ) ;
CUTBoolean cutWriteFiled  ( const char * filename, const double        * data,
 unsigned int len, double        epsilon, bool verbose = false ) ;
CUTBoolean cutWriteFilei  ( const char * filename, const int           * data,
 unsigned int len, int           epsilon, bool verbose = false ) ;
CUTBoolean cutWriteFileui ( const char * filename, const unsigned int  * data,
 unsigned int len, unsigned int  epsilon, bool verbose = false ) ;
CUTBoolean cutWriteFileb  ( const char * filename, const char          * data,
 unsigned int len, char          epsilon, bool verbose = false ) ;
CUTBoolean cutWriteFileub ( const char * filename, const unsigned char * data,
 unsigned int len, unsigned char epsilon, bool verbose = false ) ;

CUTBoolean cutLoadPGMub  ( const char * file, unsigned char  ** data, unsigned int * w,
 unsigned int * h ) ;
CUTBoolean cutLoadPPMub  ( const char * file, unsigned char  ** data, unsigned int * w,
 unsigned int * h ) ;
CUTBoolean cutLoadPPM4ub ( const char * file, unsigned char  ** data, unsigned int * w,
 unsigned int * h ) ;

CUTBoolean cutLoadPGMi   ( const char * file, unsigned int   ** data, unsigned int * w,
 unsigned int * h ) ;

CUTBoolean cutLoadPGMs   ( const char * file, unsigned short ** data, unsigned int * w,
 unsigned int * h ) ;

CUTBoolean cutLoadPGMf   ( const char * file, unsigned float ** data, unsigned int * w,
 unsigned int * h ) ;

CUTBoolean cutSavePGMub  ( const char * file, unsigned char  * data, unsigned int w, unsigned int h ) ;
CUTBoolean cutSavePPMub  ( const char * file, unsigned char  * data, unsigned int w, unsigned int h ) ;
CUTBoolean cutSavePPM4ub ( const char * file, unsigned char  * data, unsigned int w, unsigned int h ) ;

CUTBoolean cutSavePGMi   ( const char * file, unsigned int   * data, unsigned int w, unsigned int h ) ;

CUTBoolean cutSavePGMs   ( const char * file, unsigned short * data, unsigned int w, unsigned int h ) ;

CUTBoolean cutSavePGMf   ( const char * file, unsigned float * data, unsigned int w, unsigned int h ) ;

IX-B-3. Gestion de la ligne de commande▲

CUTBoolean cutCheckCmdLineFlag ( const int argc, const char ** argv, const char * flag_name ) ;

CUTBoolean cutGetCmdLineArgumenti   ( const int argc, const char ** argv, const char * arg_name,
    int   * val ) ;
CUTBoolean cutGetCmdLineArgumentf   ( const int argc, const char ** argv, const char * arg_name,
    float * val ) ;
CUTBoolean cutGetCmdLineArgumentstr ( const int argc, const char ** argv, const char * arg_name,
    char ** val ) ;

IX-B-4. Comparaison▲

CUTBoolean cutComparef  ( const      float    * reference, const      float    * data,
    const unsigned int len ) ;
CUTBoolean cutComparei  ( const       int     * reference, const       int     * data,
    const unsigned int len ) ;
CUTBoolean cutCompareub ( const unsigned char * reference, const unsigned char * data,
    const unsigned int len ) ;

CUTBoolean cutComparefe ( const float * reference, const float * data, const unsigned int len,
    const float epsilon ) ;

IX-B-5. Gestion du temps▲

CUTBolean cutCreateTimer   (       unsigned int * name ) ;
CUTBolean cutDeleteTimer   (       unsigned int   name ) ;
CUTBolean cutStartTimer    ( const unsigned int   name ) ;
CUTBolean cutStopTimer     ( const unsigned int   name ) ;
CUTBolean cutResetTimer    ( const unsigned int   name ) ;
CUTBolean cutGetTimerValue ( const unsigned int   name ) ;

 

Cacher/Afficher le codeSélectionnez

int main()
{
    float *h_A, *h_B, *h_C_GPU;
    float *d_A, *d_B, *d_C;
    unsigned int hTimer;
    int i, j;
    
    int VECTOR_N  = 512;
    int    DATA_N = VECTOR_N;
    int   DATA_SZ = DATA_N    * sizeof(float);
    int RESULT_SZ = VECTOR_N  * sizeof(float);
    CUT_DEVICE_INIT();
    CUT_SAFE_CALL( cutCreateTimer(& hTimer) );

    printf("Initializing data...\n");
        printf("...allocating CPU memory.\n");
        h_A     = (float *) malloc(DATA_SZ);
        h_B     = (float *) malloc(DATA_SZ);
        h_C_GPU = (float *) malloc(RESULT_SZ);

        printf("...allocating GPU memory.\n");
        CUDA_SAFE_CALL( cudaMalloc( (void **) & d_A, DATA_SZ)   );
        CUDA_SAFE_CALL( cudaMalloc( (void **) & d_B, DATA_SZ)   );
        CUDA_SAFE_CALL( cudaMalloc( (void **) & d_C, RESULT_SZ) );

        printf("...generating input data in CPU mem.\n");
        srand(153);
        for(i = 0 ; i < DATA_N ; i++)
        {
            h_A[i] = RandFloat(0.0f, 1.0f);
            h_B[i] = RandFloat(0.0f, 1.0f);
        }

        printf("...copying input data to GPU mem.\n");
        CUDA_SAFE_CALL( cudaMemcpy(d_A, h_A, DATA_SZ, cudaMemcpyHostToDevice) );
        CUDA_SAFE_CALL( cudaMemcpy(d_B, h_B, DATA_SZ, cudaMemcpyHostToDevice) );
    printf("Data init done.\n");

    printf("Executing GPU kernel...\n");
       CUDA_SAFE_CALL( cudaThreadSynchronize() );
        CUT_SAFE_CALL( cutResetTimer(hTimer) );
        CUT_SAFE_CALL( cutStartTimer(hTimer) );
        scalarProdGPU <<<1, VECTOR_N>>> (d_C, d_A, d_B, VECTOR_N);
        CUT_CHECK_ERROR("scalarProdGPU() execution failed\n");
        CUDA_SAFE_CALL ( cudaThreadSynchronize() );

    printf("Reading back GPU result...\n");
        CUDA_SAFE_CALL( cudaMemcpy(h_C_GPU, d_C, RESULT_SZ, cudaMemcpyDeviceToHost) );
        CUT_SAFE_CALL ( cutStopTimer(hTimer) );
    printf("GPU time: %f msecs.\n", cutGetTimerValue(hTimer));
    
    printf("Shutting down...\n");
        CUDA_SAFE_CALL( cudaFree(d_C) );
        CUDA_SAFE_CALL( cudaFree(d_B)   );
        CUDA_SAFE_CALL( cudaFree(d_A)   );
        free(h_C_GPU);
        free(h_B);
        free(h_A);
        CUT_SAFE_CALL( cutDeleteTimer(hTimer) );
}

Ceci ne présente que l'utilisation de fonctions et de macros CUTIL. Des fonctions utilisées sont définies dans le fichier completet dans les kernels.

Les fonctions et macros CUTIL sont définies dans le fichier cutil.h.