I. Définition du modèle de décisions▲
Après avoir discuté de la notion de modèle de décisions et de leur utilité, mais également de leurs limitations, une illustration des concepts de base avec un exemple simple s'impose.
Cependant, avant de continuer, il sera intéressant d'introduire un plan et des recommandations de formatage. Tout comme le code, les feuilles de calcul peuvent se transformer rapidement en un amas de nombres difficilement lisible, à moins d'y prêter une attention suffisante.
De manière générale, les cellules des feuilles de calcul se séparent en quatre catégories :
- les cellules de décision contiennent les variables à optimiser : en d'autres mots, l'objectif du solveur sera de déterminer les valeurs optimales pour ces cellules. Leur valeur initiale sera nulle ou toute autre valeur appropriée, le rôle du solveur sera de remplacer ces données initiales par leur valeur optimale. Dans la plupart des cas, les valeurs seront contraintes dans un certain intervalle, par exemple entre un minimum et un maximum ; dans certains cas, ces valeurs devront être binaires ou entières. Pour assurer une certaine cohérence et garantir la lisibilité, les cellules de décision seront toujours en jaune et entourées d'une ligne noire ;
- les cellules prédéfinies ont leur valeur déterminée par le problème. Par exemple, si une sucette pèse dix-sept grammes et chaque coup de langue en enlève un quart de gramme, ce seront des données prédéfinies. Ces cellules auront pour couleur le bleu ;
- les cellules de calcul sont calculées depuis d'autres valeurs de la feuille de calcul et ne correspondent à aucune autre catégorie. Elles seront peintes en gris ;
- la cellule de l'objectif (ou de sortie) contiendra la valeur à maximiser ou à minimiser lors du lancement de l'optimiseur. Dans les exemples, il n'y aura jamais qu'une seule et unique cellule d'objectif ; elle sera toujours colorée en orange et entourée par un trait noir épais. (Certains solveurs autorisent plusieurs objectifs, mais leur emploi est bien plus compliqué, sans qu'ils soient utiles dans les cas étudiés.)
À son lancement, l'optimiseur (l'outil « Solveur » d'Excel) regardera la cellule d'objectif identifiée et tentera de modifier les variables de décisions autant qu'il peut (en respectant les contraintes imposées) pour minimiser ou maximiser cette cellule d'objectif (selon l'ordre qui lui est donné).
Le solveur ne connaît pas grand-chose du type de calculs qui se passe ou la connexion entre les cellules de décision et de sortie : il lance simplement un des algorithmes à sa disposition pour minimiser ou maximiser la valeur de la cellule d'objectif grâce à une recherche des valeurs possibles des cellules de décision. Ces algorithmes (simplexe, GRG non linéaire, évolutionnaire) sont conçus pour être bien plus intelligents qu'une exploration par force brute de tous les choix possibles pour les variables de décision : ils peuvent souvent donner des réponses rapidement à des problèmes de grande taille.
Par exemple, pour déterminer le nombre de coups de langue à donner à la sucette pour la finir, la feuille de calcul pourrait ressembler à ceci :
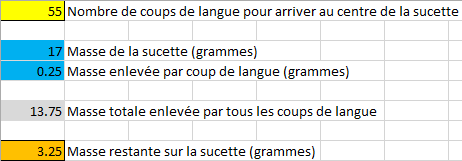
Il serait possible d'utiliser le solveur d'Excel pour résoudre ce problème, en lui demandant de minimiser la valeur de la cellule contenant la masse restante sur la sucette : il trouverait rapidement que la valeur de la décision en jaune pour ce faire est de soixante-huit.
Cependant, utiliser un tel outil pour ce genre de problème est absurde, car l'énoncé du problème indique directement que la solution est kitxmlcodeinlinelatexdvp17/0,25 = 68finkitxmlcodeinlinelatexdvp. Il n'y a pas besoin de lancer un outil d'optimisation pour un problème abordable avec des opérations arithmétiques de base.
En pratique, cependant, la plupart des problèmes n'auront pas de solution mathématique simple. Ils posséderont un certain nombre de variables de décision qui ne font pas évoluer l'objectif de manière évidente : cette correspondance entre les décisions et l'objectif sera trop compliquée pour résoudre le problème à la main avec un ensemble d'équations facilement identifiables. Pour rappel, les mathématiques compliquées seront évitées avec soin dans cette série d'articles : le centre d'intérêt sera la modélisation des problèmes, le solveur pourra se charger de ces aspects plus compliqués.
II. Premier exemple : les taxes▲
Le premier vrai modèle de décision concernera la détermination d'un taux de taxation optimal. Personne n'aime les taxes, mais, dans ce cas, le joueur les reçoit et ne les paie donc pas, ce qui diminue quelque peu la douleur.
Le contexte est celui d'un jeu de stratégie de type 4X comme Sid Meier's Civilization, lors de l'ébauche des villes. Leur niveau de malheur dépend notamment de leur taille. Les citoyens malheureux ne sont pas coopératifs, ils ne payent pas leurs taxes. Le joueur peut récolter de l'argent de ses villes en ajustant le niveau de taxes ville par ville, mais le niveau de malheur d'une ville grandit de manière exponentielle avec les taxes : de hauts niveaux de taxes peuvent être contre-productifs.
Par hypothèse, le niveau de taxes peut varier par incréments de dix pour cent entre zéro et cinquante pour cent. Par exemple, le classique Master of Orion 2 présente un système similaire :
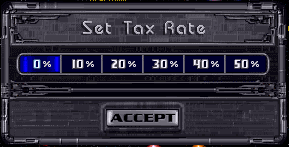
Le concepteur du jeu peut se poser une question simple : quel est le niveau de taxes optimal dans le cas général ?
Ce devrait être un problème relativement simple, puisqu'il n'y a que six choix possibles. Une solution simple serait de tester les six choix à la main et de choisir celui qui donne les meilleurs revenus.
En fait, il est probablement possible de trouver une formulation à partir d'équations mathématiques pour trouver cette solution, comme dans l'exemple précédent, mais cela ne servirait pas l'objectif de l'article, puisqu'il est d'atteindre des modèles plus compliqués qui ne peuvent pas être résolus de la sorte. De toute façon, cette série tente d'éviter les mathématiques autant que possible.
La première étape est de poser le problème.
- La ville a une taille de douze unités (ce qui correspond à douze millions de personnes). Ces personnes sont représentées comme douze « citoyens ».
- À tout moment, chaque citoyen est soit heureux soit malheureux.
- Les citoyens heureux payent des taxes, le décuple du taux de taxes. Par exemple, un taux de taxes de vingt pour cent donne deux unités monétaires de revenus par citoyen heureux. A contrario, les citoyens malheureux ne paient pas de taxes.
- La ville possède trois citoyens malheureux : peu importe le niveau de taxes, ils resteront malheureux.
- Un nombre supplémentaire de citoyens deviendra malheureux selon le produit de la population, du carré du niveau de taxes et d'un facteur 3,5, arrondi à l'entier inférieur. Ainsi, pour la ville de douze citoyens, des taxes entre zéro et dix pour cent ne donneront aucun nouveau citoyen malheureux ; un à vingt pour cent, trois à trente, six à quarante et dix à cinquante.
Simple, non ?
Dans cette formulation, la cellule de décision (niveau de taxes) est une manière indirecte de spécifier le taux de taxation : au lieu de donner directement le niveau de taxes dans la cellule de décision, le calcul du taux prend un nombre de la cellule de décision et le multiplie par dix pour cent. Il y a une bonne raison de le faire, qui deviendra claire dans un instant.
Pour le moment, la feuille de calcul permet l'expérimentation, notamment le test de chacune des six valeurs pour le niveau de taxes. Insérer chacun des six niveaux possibles donne le tableau suivant.
| Niveau de taxes | Revenu des taxes |
|---|---|
| 0 % | 0 |
| 10 % | 9 |
| 20 % | 16 |
| 30 % | 18 |
| 40 % | 12 |
| 50 % | 0 |
La réponse saute aux yeux : il existe un niveau optimal pour les taxes, trente pour cent, ce qui correspond à un revenu de dix-huit unités monétaires.
III. Automatisation▲
Ce procédé fonctionne bien, mais que se passe-t-il s'il y avait plus de six possibilités ? Par exemple, des centaines de niveaux de taxes ou d'autres paramètres. La situation deviendrait vraiment compliquée.
Le solveur sert exactement dans ce genre de situations.
La première étape est de revenir à un niveau de taxe nul. Ensuite, dans l'onglet Données, la case Analyse devrait présenter un bouton Solveur.
S'il n'est pas visible, il faut l'activer. Dans le menu Office, les options d'Excel proposent une catégorie « Compléments » : dans la zone « Gérer », sélectionner « Compléments Excel », s'assurer que la case « Complément Solveur » est bien cochée.
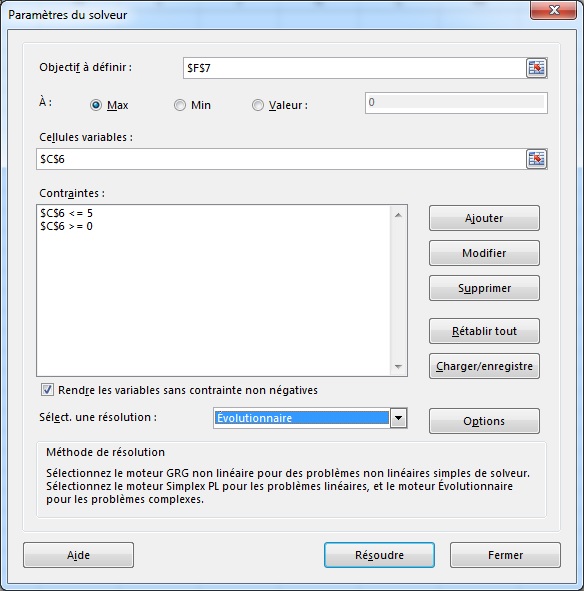
En appuyant sur ce bouton Solveur, une boîte de dialogue comme celle-ci devrait apparaître.
Le champ « Cellule cible » correspond à la cellule à optimiser. Dans ce cas, l'objectif est d'obtenir le plus de taxes possible, cette cellule est donc l'objectif en orange, soit le revenu des taxes, qui doit être maximisé.
Les « Cellules variables » sont celles que le solveur devrait déterminer. Ici, il s'agit de la cellule en jaune. Si tout se passe comme prévu, le solveur devrait mettre la valeur trois dans cette case, ce qui correspond à un niveau de trente pour cent, ce qui correspond à la valeur optimale.
Finalement, il faut ajouter quelques contraintes. Elles agissent comme des conditions sur toute cellule du modèle de décision ; le solveur d'Excel s'assurera de ne vérifier que des solutions qui respectent ces contraintes. Elles peuvent limiter des cellules spécifiques (souvent, des cellules de décision ou de calcul) à une plage de valeurs ou bien les forcer à prendre une valeur entière ou binaire (un ou zéro). Les contraintes sont extrêmement utiles pour assurer la validité du modèle.
Le solveur a besoin d'au moins quelques contraintes pour déterminer les limites des cellules de décision : en d'autres mots, le maximum et le minimum pour chaque cellule. Le bouton « Ajouter » sert à insérer une nouvelle contrainte.
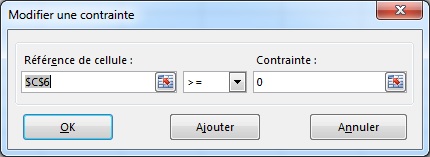
Pour ce modèle, deux contraintes sont nécessaires : le niveau de taxes doit être supérieur ou égal à zéro, la cellule de décision doit être inférieure ou égale à cinq. Ensuite, en choisissant l'algorithme évolutionnaire comme méthode de résolution, il suffit de lancer le solveur pour obtenir la solution.
Après une trentaine de secondes, il donne une réponse intéressante :

Il y a donc un problème. Le solveur a obtenu le même revenu, mais le niveau de taxes est mauvais, puisque le joueur ne peut utiliser que des incréments de dix pour cent.
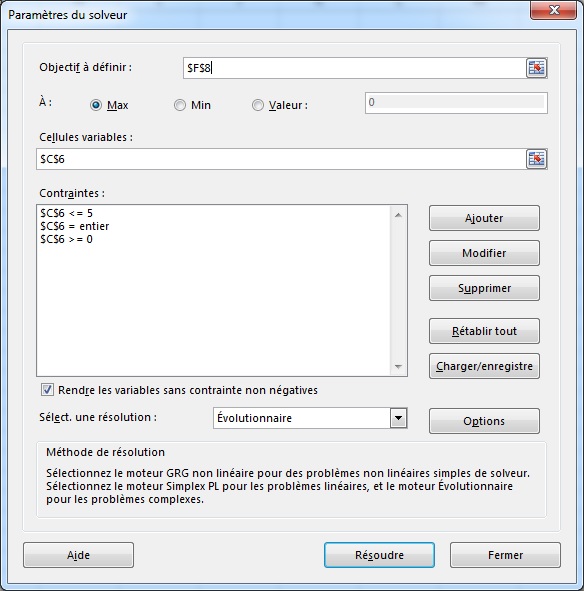
La solution est de s'assurer que la cellule du niveau de taxe reste un nombre entier. Elle devrait avoir pour valeur zéro, un, deux, trois, quatre ou cinq, pas une valeur intermédiaire.
Heureusement, le solveur propose une manière simple pour ce faire : ajouter une nouvelle contrainte. En appuyant à nouveau sur le bouton « Ajouter » et en sélectionnant la cellule de décision correspondant au niveau de taxes, il suffit de sélectionner la contrainte « ent ».
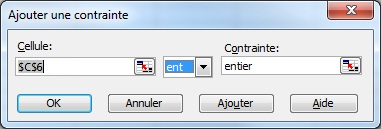
Maintenant, en relançant le solveur, la nouvelle solution est :

Le solveur a obtenu la même réponse que précédemment, avec très peu d'efforts. Comme la suite le montrera, pour des problèmes de plus grande taille, la quantité de travail que le solveur peut abattre dépasse largement le temps requis pour lui indiquer ce qu'il doit faire.
IV. Croissance de la ville▲
Pour rendre la situation plus intéressante, le modèle est à présent généralisé.
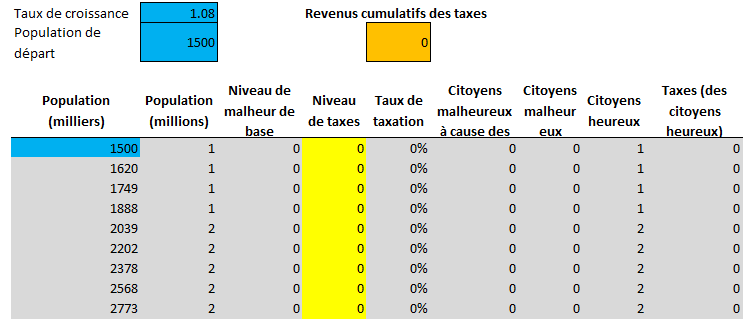
Dans tout jeu de stratégie de type 4X, les villes (planètes, colonies, etc.) grandissent avec le temps. Par hypothèse, la ville aura un taux de croissance de huit pour cent par tour, en commençant à un million et demi de citoyens, jusqu'à atteindre douze millions. La feuille de calcul ressemble désormais à ceci :
Chaque ligne du tableau correspond à un tour dans le jeu.
Le calcul du nombre de base de citoyens malheureux a aussi changé : il s'agit maintenant de la moitié de la population de base (exprimée en millions) arrondie à l'entier inférieur. Ainsi, le nombre de malheureux est nul jusqu'à une taille de quatre ; après, il grandit de manière linéaire avec la taille de la ville.
Comme précédemment, les revenus des taxes peuvent être maximisés en tenant manuellement les divers niveaux : pour des taux entre 0 et 50 %, les résultats sont de 0, 102, 190, 222, 144 et 65 unités monétaires.
Tout comme précédemment, le solveur peut également résoudre ce problème : la solution optimale est toujours un niveau de taxe de trente pour cent, pour un revenu total de deux cents vingt-deux unités monétaires. Les paramètres du solveur sont ceux-ci :
V. Taux de taxes variable▲
Cependant, bien évidemment, le joueur n'agit pas de la sorte : la ville ainsi simulée n'a qu'un seul taux de taxes, constant tout au long de la partie. Le joueur peut cependant changer ce niveau aussi souvent qu'il le souhaite : il le fera d'ailleurs probablement pour s'adapter à la croissance de la ville et aux circonstances.
Il serait bien de déterminer plus qu'un seul et unique taux de taxation, plutôt une valeur optimale pour chaque tour. Ainsi, le solveur donnerait le comportement d'un excellent joueur par rapport aux taxes de cette ville. Bien évidemment, cette modification est possible : maintenant que le modèle de décision est bien installé, elle se révèle extrêmement facile.
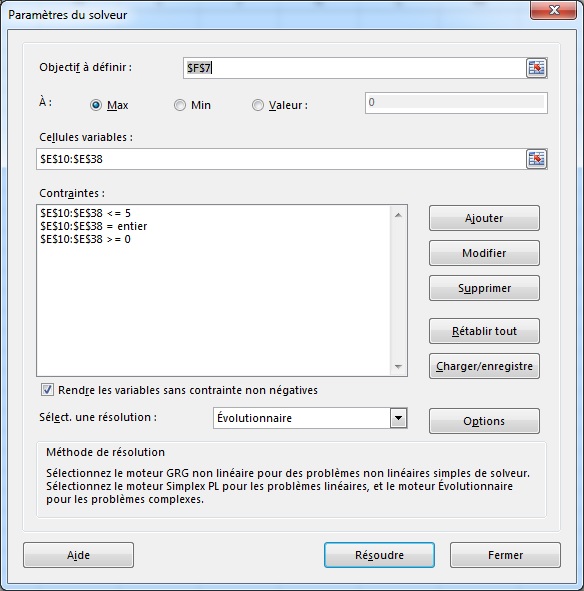
Le changement principal est la suppression de la cellule de décision du niveau de taxes : elle est remplacée par une colonne entière de niveaux de taxes, un par tour.
Au lieu de demander au solveur d'optimiser la valeur d'une seule cellule, il devra gérer toute une colonne. Ses paramètres évoluent donc en fonction : les seuls changements sont les cellules variables et les contraintes, qui représentent maintenant toute la colonne des niveaux de taxation au lieu d'une simple cellule.
Le solveur indique maintenant que changer plus fréquemment le niveau de taxes donne un avantage au joueur, avec un revenu cumulé de deux cents trente-deux unités. Bien qu'il ne s'agisse que d'une amélioration de cinq pour cent par rapport à la situation précédente, certains joueurs vont l'atteindre.
La solution obtenue commence avec un taux de cinquante pour cent, puisqu'une ville très petite n'a pas assez de population pour générer du mécontentement. Au fur et à mesure de la croissance de la ville, cette solution optimale oscille entre vingt et trente pour cent, selon le choix qui amène le plus de revenus.
La feuille de calculs correspondante est disponible au téléchargement : elle sépare les trois étapes de cet exemple en trois feuilles de travail distinctes (une population fixe, une population croissante, un niveau de taxe ajustable).
VI. Conclusions▲
La solution trouvée révèle une caractéristique intéressante : la nature discrète du jeu de simulation, qui représente des groupements arbitraires de millions de personnes comme des « citoyens » heureux ou non, introduit des particularités dans le modèle. Bien que le jeu lui-même ait besoin de cette discrétisation à un moment ou à un autre pour l'accessibilité et la jouabilité, les joueurs intelligents pourront exploiter cette granularité artificielle pour générer des avantages par rapport à des joueurs qui ne veulent pas s'occuper du niveau de taxes chaque tour.
Cette remarque soulève une question intéressante sur la conception du jeu : cet effet est-il souhaité ? Les mécaniques du jeu forceront-elles les joueurs à gérer de manière fine les niveaux de taxes pour chaque tour ? Est-il souhaitable que les joueurs les plus avancés puissent utiliser le jeu de cette manière ? La récompense de cinq pour cent est-elle appropriée ?
Il est impossible d'y apporter des réponses définitives : après tout, vous êtes le concepteur, c'est à vous de décider des objectifs du jeu, de déterminer si ce niveau d'exploitation est en accord avec vos objectifs.
Bien évidemment, ce modèle est assez pauvre. Dans un vrai jeu de stratégie 4X, le joueur dispose de bien d'autres décisions sur la manière de faire grandir la cité, sur les constructions et autres modifications qui affectent la croissance de la ville, le niveau de bonheur, les taxes et la productivité.
Un prochain article de cette série montrera un modèle similaire mais bien plus complexe d'une planète colonisée complète dans un jeu similaire à Master of Orion 2. Cet exemple sera bien plus sophistiqué, puisqu'il pourra prendre, chaque tour, des décisions qui affecteront tous ces paramètres, comme la croissance et la productivité, de telle sorte que chaque décision a des effets sur les décisions suivantes. Cet exemple montrera également que l'algorithme évolutionnaire du solveur est capable de relever le défi.
Le prochain épisode de cette série s'occupera du chargement des armes dans SuperTank, l'exemple posé dans l'introduction.
VII. Remerciements▲
L'auteur souhaiterait remercier Robert Zubek et Jurie Horneman pour leurs retours sur cet article. Le professeur Christopher Thomas Ryan, Assistant Professor of Operations Management à la University of Chicago Booth School of Business, a également participé à la révision de ce texte.
Cet article est une traduction autorisée de Decision Modeling and Optimization in Game Design, Part 2: Optimization Basics and Unrolling a Simulation, écrit par Paul Tozour. Le traducteur souhaiterait remercier Alexandre Laurent pour sa relecture, ainsi que Jean-Philippe André pour sa relecture et les captures d'écran d'Excel en français.