Modélisation et optimisation des décisions dans la conception de jeux

Une question se soulève naturellement : que se passe-t-il pour l'équilibrage d'un jeu ? Est-il possible d'appliquer ces techniques aux délicats problèmes d'équilibrage que l'on trouve dans beaucoup de types de jeux, comme les jeux de stratégie, les jeux de rôle, y compris en ligne ?

La réponse est positive, évidemment, mais avec quelques mises en garde. En particulier, les feuilles de calcul se révèlent fort limitées, parce que, dans la plupart des cas non triviaux, elles ne peuvent représenter précisément le jeu. Ce défaut d'expressivité rend difficile leur utilisation à des fins d'équilibrage robuste avec des techniques d'optimisation ; les problèmes réalistes d'équilibrage présent dans la très grande majorité des jeux seront très en dehors du champ de modélisation d'une feuille de calcul. La seule simulation d'un jeu est souvent déjà trop complexe : elle possède un très grand nombre d'éléments dynamiques et se déroule en temps réel, ce qui ajoute des obstacles à toute simulation discrète.

Ainsi, pour utiliser ces techniques d'équilibrage dans le cadre de MMORPG comme WildStar ou de jeux de stratégie comme Planetary Annihilation, il faudrait les intégrer dans la simulation du jeu elle-même, sans quoi elles seraient imprécises et inutiles.

Aussi, certains aspects de l'équilibrage ne peuvent pas être automatisés : comme indiqué dès le premier article, il n'est pas possible de modéliser le ressenti face à un jeu.

Par conséquent, le mieux que l'on peut faire est de montrer un exemple simple pour illustrer l'approche globale à ce genre de problèmes, la manière de mettre en forme ce type de problème et de les optimiser à l'aide d'Excel. Dans le cas relativement simple d'un combat, le solveur peut effectuer un très bon travail d'équilibrage des différentes classes de personnages. Cette structure de base peut alors servir comme architecture de ce type de problème d'optimisation dans des cas plus généraux, bien intégrés aux mécanismes de jeu.

Cela étant dit, cet article est écrit dans l'espoir de traverser ces limitations, pour voir jusqu'où un exemple peut mener.

Il n'existe pas de définition unique et largement acceptée du mot « équilibrage ». Il possède un grand nombre de significations : le vrai sens dépend du contexte du jeu en question. Selon les conditions, cet « équilibrage » peut faire référence à la détermination des caractéristiques des différentes classes de personnages pour que leurs capacités soient équivalentes dans un jeu de rôle ou d'action en équipe, mais aussi à la compensation des forces qui s'opposent dans un jeu de stratégie ou encore à l'ajustage des coûts des unités ou ressources afin de les lier à leur utilité, entre autres.

La meilleure définition de l'équilibrage dépend souvent des objectifs de la conception du jeu en question. Puisque ces objectifs ne peuvent pas être restreints a priori, il n'est pas possible de déterminer à l'avance ce que l'équilibrage peut être pour des jeux en général, en dehors d'un genre particulier.

Certains joueurs ont l'idée préconçue que l'équilibrage d'un combat signifie des dégâts égaux. C'est particulièrement vrai dans le cas de jeux de rôle massivement multijoueurs (MMORPG), où les joueurs se plaignent souvent que la quantité de dommages par seconde (DPS) d'une classe est trop faible ou trop élevée par rapport à une autre. Évidemment, les classes ne peuvent pas être équilibrées en ne regardant que ces DPS : il est parfaitement valide qu'une classe cause plus de dommages par unité de temps qu'une autre si cet avantage est compensé par d'autres facteurs qui limitent l'utilité générale de la classe, comme une capacité à survivre diminuée ou moins de dommages causés sur le long terme, malgré des pointes.

Cet article développera l'exemple d'un nouveau jeu de rôle en ligne, fortement simplifié, nommé « Petit MMO ». L'objectif est d'équilibrer quatre classes pour des combats de type joueur contre joueur de telle sorte que, même différentes, les quatre classes aient des capacités similaires dans un combat contre d'autres, qu'il n'existe pas de « meilleure » ou de « pire » classe.

Bien que « Petit MMO » soit un jeu en temps réel, chaque action d'un joueur dure exactement trois secondes, de telle sorte qu'un combat peut être discrétisé en le représentant au tour par tour, chacun représentant trois secondes de jeu.

Dans ce jeu, les joueurs pourront incarner l'une des quatre classes suivantes.

• Le guerrier effectue le plus de dommages.
• Le mage lance des sorts à distance : il a la portée la plus grande des quatre.
• Le guérisseur se soigne automatiquement pour une certaine quantité de points de vie chaque tour.
• Le barbare a le plus de points de vie des quatre classes.

Ces caractéristiques sont les seules connues des quatre classes : il faut définir les points de vie initiaux, les dommages, les capacités de soin et les rayons d'action de chacune des quatre classes. Ces caractéristiques doivent être équilibrées, de telle sorte que chaque classe soit unique et que ses caractéristiques soient franchement différentes des autres classes, tout en s'assurant que chacune soit aussi « équilibrée » que possible par rapport aux trois autres classes.

En d'autres termes, il s'agit d'optimiser la table suivante.

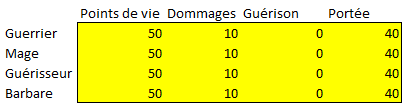
Pour le moment, les valeurs données sont arbitraires : chaque classe aura cinquante points de vie, infligera dix points de dommages par tour lors d'une attaque, ne se soignera pas et aura une portée de quarante mètres. Chaque unité pourra se déplacer de cinq mètres par tour. Puisque les spécifications de conceptions impliquent que les quatre classes se meuvent à la même vitesse, ce fait sera considéré comme fixé : la vitesse de déplacement ne sera pas considérée dans la table des variables de décision.

Certes, cet exemple est simplifié, avec des données schématiques. Les dommages sont une moyenne continue sur un tour, qui ignore tout pic et tout effet sur le long terme qui accompagne le mana ou d'autres mécanismes qui modifient les capacités d'attaque des classes. Il n'y a qu'un seul type de dommages, ce qui n'est pas très réaliste puisque la majorité des classes en ont plusieurs types, voire plusieurs dizaines : il faudrait implémenter un système d'intelligence artificielle pour décider de l'attaque à utiliser chaque tour. Aussi, les dommages ont souvent une composante aléatoire dans la plupart des jeux, mais elle sera ignorée pour le moment : la variance des dommages ne sera pas suffisamment grande pour avoir du sens au moment du dénouement du combat, peu importe les classes considérées.

Évidemment, tout équilibrage effectué dans Excel n'a pratiquement aucune chance d'être parfait ou de correspondre à l'équilibrage final du jeu : cette phase n'éclipse pas les tests réels. Par contre, si cette technique donne, en quelques heures de travail, une bonne estimation des paramètres pour un jeu aussi simple dans Excel, au moins, il est probable qu'elle approche le concepteur de valeurs solides pour une première passe d'équilibrage, ce qui l'amènera plus près du résultat final.

L'équilibrage des quatre classes se fait dans le contexte de combats entre deux joueurs. Puisqu'il n'y a que quatre classes (guerrier, mage, guérisseur, barbare), six situations doivent être vérifiées :

• guerrier contre mage ;
• guerrier contre guérisseur ;
• guerrier contre barbare ;
• mage contre guérisseur ;
• mage contre barbare ;
• soigneur contre barbare.

Ce type d'équilibrage peut être extrêmement difficile. Même dans ce cas extrêmement simple, six relations entre classes doivent être étudiées, comme les six lignes qui peuvent être dessinées entre les quatre sommets d'un carré.

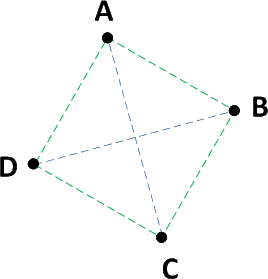
Tout changement effectué, même minime, sur les paramètres d'une seule classe aura un impact sur l'équilibrage par rapport à toutes les autres classes. Cette interconnexion complète n'augmente qu'avec le nombre de classes. Les décisions prises pour l'équilibrage d'une paire peuvent être dangereuses tant qu'il est considéré dans l'absolu, sans prendre le temps d'observer l'effet sur l'équilibrage par rapport aux autres paires.

Idéalement, le résultat du processus d'optimisation devrait donner une table des victoires similaire à celle-ci. En modélisant le combat pour chacune des six paires dans la feuille de calcul, il devient possible de générer une forme de « score » pour chacune des six paires. Puisque de meilleurs scores sont toujours meilleurs, leur combinaison pourrait former la fonction objectif.

Dans cette table, les éléments sur la diagonale sont nuls, parce qu'ils représentent un combat d'une classe contre elle-même, une situation déjà équilibrée par définition. De même, les cellules dans le coin en haut à droite sont également toutes nulles, puisqu'elles représentent les mêmes situations que les cellules en bas à gauche.

Maintenant, il est temps de définir un modèle de combat entre une classe et une autre.

Chaque combat verra ses adversaires placés à cent mètres l'un de l'autre. Chaque personnage prendra trois secondes pour attaquer, la situation peut donc se représenter au tour par tour, chaque « tour » prenant trois secondes. Chaque « tour », les unités pourront soit attaquer l'autre si elle est dans la portée, soit continuer à s'en approcher jusqu'à pouvoir l'attaquer.

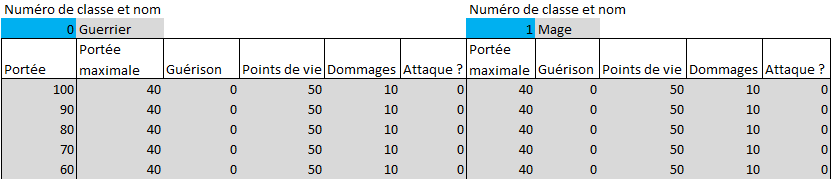
La simulation ressemble donc à ceci.

Au-dessus des titres, la paire d'unités s'affrontant est désignée. Dans ce cas, il s'agira d'un combat entre un guerrier et un mage. La colonne de gauche montre la distance entre les deux unités simulées.

Pour chaque unité, une série de colonnes est présentée.

• La portée maximale correspond à la portée maximale à laquelle l'unité peut attaquer. Cette valeur est déterminée directement de la variable de décision en jaune.
• La guérison est le nombre de points de vie que l'unité récupère chaque tour, également tirée directement de la variable de décision correspondante.
• Les points de vie représentent la quantité de dommage que chaque unité peut subir, tour par tour. Elle commence comme le nombre de points de vie des variables de décision, mais se réduit au fil du combat, au fur et à mesure des attaques. Cette valeur est également incrémentée quand l'unité se soigne.
• Les dommages correspondent aux points de vie que l'unité peut faire perdre à l'ennemi en un tour quand il est dans son rayon d'action. Ils deviennent nuls dès la défaite du personnage.
• La dernière cellule indique si une unité attaque l'autre quand elle est à portée de tir. Si oui, la valeur affichée est « 1 », ce qui indique que l'unité attaque ce tour-là ; sinon, ce sera un « 0 », l'unité se déplacera pour s'approcher de l'ennemi.

De cette manière, les deux unités commenceront à se déplacer l'une vers l'autre ; ensuite, elles attaqueront jusqu'au décès d'une ou des deux. Puisque chaque unité se déplace à la vitesse de cinq mètres par trois secondes, la distance décroît de dix mètres à chaque tour tant que les deux unités marchent l'une vers l'autre, puis cinq les tours où seule une des deux unités marche vers l'autre. Le jeu lui-même est conçu de telle sorte que les deux unités peuvent entreprendre un mouvement au même instant et que cette action ait lieu simultanément, il est donc entièrement possible que les deux unités soient mortes en même temps.

Ensuite, il faut définir le score pour ce tableau et générer une valeur numérique qui indique à quel point le combat fut « bon » - en d'autres termes, sa proximité par rapport aux objectifs de conception.

Clairement, les deux unités devraient être mortes à la fin du combat ou, au moins, aussi près que possible de la mort. Si le combat est équilibré, alors les deux classes en compétition devraient faire descendre le niveau de vie de l'autre aussi bas que possible à la fin du combat.

Cependant, cela ne sera pas suffisant. Si le score est effectivement calculé de cette manière, l'optimiseur augmentera juste les dommages autant que possible, de telle sorte que les deux unités se tuent mutuellement instantanément. Les plus curieux peuvent d'ores et déjà tenter de visualiser ce comportement sur la feuille de calcul. Ce n'est pas l'objectif du jeu : les deux unités devraient décéder ou être dans un état critique à la fin du combat, mais celui-ci devrait également durer un certain temps.

En d'autres mots, le but n'est pas seulement d'équilibrer les classes de manière relativement équitable ; il comporte aussi un équilibre sur l'intérêt, dont une grande partie repose sur la durée des combats.

Pour générer ce score, il faut encore définir quelques cellules à la droite de chaque tableau. La durée indique le nombre de tours du combat, calculé comme le nombre de lignes dans le tableau où les deux unités sont en vie. Les points de vie totaux cumulent les points restants pour chacune des deux unités ; idéalement, cette valeur devrait être nulle, c'est-à-dire que les deux unités sont mortes à la fin du combat.

Finalement, le score combine ces deux indicateurs, sous la forme (Durée / (1 + Points de vie totaux)). Le terme +1 au dénominateur est requis dans le cas où le total des points de vie est nul : sans lui, le dénominateur serait nul, ce qui donnerait une erreur arithmétique de division par zéro. De cette manière, la récompense pour l'optimiseur serait maximale dans le cas où le combat a une durée maximale et très peu de points de vie restants.

À cause des limitations des tableurs, le nombre de lignes est fixé d'avance (ici, chaque simulation dure à dix-sept lignes) : il s'agit d'un choix de conception qui indique que les combats devraient durer approximativement dix-sept tours. Pour leur imposer d'être plus longs ou plus courts, il est possible de changer ce nombre de lignes, en ajustant les formules de score pour correspondre aux nouvelles données.

Finalement, ces six valeurs de score (une par tableau de simulation) sont reprises dans le tableau des victoires pour montrer les résultats des combats pour toute paire de classes.

Il serait possible de simplement additionner ces six valeurs pour obtenir l'objectif final. Cependant, en procédant de la sorte, il est très probable que le solveur n'atteigne pas un bon équilibre entre le plus haut et le plus bas score pour tous les combats individuels, plutôt de très hauts scores pour certaines paires et de plus bas pour d'autres. Ce n'est à nouveau pas l'objectif de conception du jeu : tous les scores devraient être élevés, en se focalisant sur leur augmentation sur tout le tableau. Pour résoudre ce problème, la somme des scores est multipliée par le plus bas score du groupe (obtenu par la fonction MIN() d'Excel), afin d'encourager le solveur à s'intéresser aux scores les plus faibles.

Ce n'est pas encore fini. En lançant l'optimiseur avec les paramètres actuels, il ne définira probablement pas les classes correctement. En fait, la solution la plus vraisemblable donne la même valeur à toutes les caractéristiques (points de vie, dommages, guérison et portée) dans la table des variables de décision.

Évidemment, le but est d'avoir des classes bien différentes : chacune doit avoir sa propre identité. Le guerrier doit causer le plus de dommages, le mage doit avoir la portée la plus grande, le guérisseur doit récupérer le plus chaque tour, le barbare doit avoir le plus de points de vie. Aussi, ces maxima ne peuvent pas avoir une trop faible marge : les classes doivent être franchement différentes, différer d'une quantité substantielle par rapport aux autres.

Pour s'assurer que tous ces critères soient satisfaits, la feuille de calcul définit un « tableau des contraintes ». Elle s'assurera que chacune des quatre classes a le bon attribut en donnant un score binaire (« 1 » si la contrainte est satisfaite, « 0 » sinon).

La colonne de « différence minimale » indique l'écart minimal qui doit exister pour l'attribut de la classe donnée par rapport à toutes les autres classes. En d'autres mots, le guerrier doit avoir au moins quatre points de vie de plus que toute autre classe, le mage, une portée au moins supérieure de dix mètres, etc.

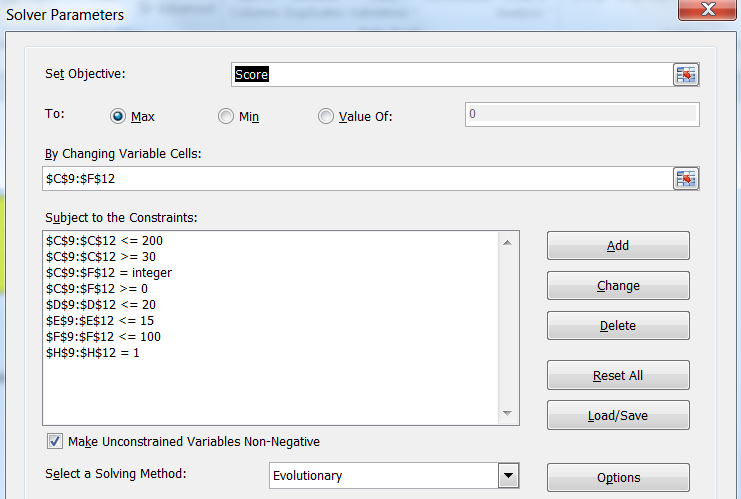
Une fois ces contraintes spécifiques entrées, il est temps de lancer l'optimisation à l'aide du Solveur d'Excel. Le deuxième article contient une introduction à cet outil et une explication pour l'activer. L'objectif sera la cellule de score, qui combine les résultats des six compétitions. Les variables de décision s'étendent aux seize cellules jaunes du tableau des variables de décision, définies au début.

Les contraintes sont ainsi définies :

• toutes les cellules doivent être entières, avec une valeur minimale nulle ;
• toutes les cellules de points de vue ont une valeur maximale de deux cents et un minimum de trente ;
• toutes les cellules de dommages ont une valeur maximale de vingt ;
• toutes les cellules de guérison ont une valeur maximale de quinze ;
• toutes les cellules de portée ont une valeur maximale de cent ;
• les quatre cellules de la table des contraintes doivent avoir une valeur unitaire pour être respectées.

La dernière étape avant de lancer le solveur est de s'assurer que l'algorithme de résolution est bien « Évolutionnaire ». Une propriété de cet algorithme est que la solution peut être améliorée en lançant le solveur une deuxième ou une troisième fois, mais aussi en modifiant ses paramètres (par le bouton « Options »).

Le résultat devrait ressembler à ceci.

Comme par magie, le solveur a donné une bonne première approximation pour l'équilibrage.

Ces solutions montrent bien que le guerrier effectue le plus de dommages, que le mage a la plus grande portée, que le guérisseur se soigne le mieux et que le barbare a le plus de points de vie. Plus bas dans la feuille de calcul, le résultat des combats entre classes détaille les différents combats : dans leur grande majorité, ils sont bien équilibrés, chacun des belligérants étant mort à la fin du combat ou bien un seul des deux survit à peine. Toutes ces simulations durent suffisamment longtemps, aucune des classes n'arrivant à abattre son adversaire en un tour.

Pas mal comme résultat obtenu en à peine quelques heures.

Cet exemple a montré un problème relativement simple d'équilibrage qui peut d'ailleurs se résoudre par simulation et optimisation. Bien qu'évidemment très limité, il montre la puissance des techniques de modélisation et d'optimisation des décisions, il pourrait aussi servir d'inspiration pour des outils plus complets d'équilibrage, plus intégrés avec les mécanismes du jeu. Au moins, il pourra servir comme un guide pour cadrer ce genre de problèmes en pratique.

Les deux prochains articles de cette série s'orienteront vers des problèmes d'assignation optimale entre deux ensembles d'entités au moins. Il s'agira de montrer comment ces types de problèmes peuvent être résolus, mais aussi comment les utiliser pour concevoir des tours pour le jeu de stratégie City Conquest, disponible sur iOS et Android.

L'auteur souhaiterait remercier Robert Zubek et Jurie Horneman pour leurs retours sur cet article. Le professeur Christopher Thomas Ryan, Assistant Professor of Operations Management à la University of Chicago Booth School of Business, a également participé à la révision de ce texte.

Cet article est une traduction autorisée de Decision Modeling and Optimization in Game Design, Part 4: Player-vs-Player Class Balancing, écrit par Paul Tozour. Le traducteur souhaiterait remercier Alexandre Laurent pour sa relecture.